Überwachtes Lernen (Supervised Learning)
Abschlussbedingungen
- Regression: Vorhersage kontinuierlicher Werte (z.B. Hauspreise).
- Algorithmen: Lineare Regression, Lasso-Regression.
- Klassifikation: Einteilung von Datenpunkten in diskrete Kategorien (z.B. E-Mail-Spam-Erkennung).
- Algorithmen: Entscheidungsbäume, Support Vector Machines (SVM), k-Nearest Neighbors (k-NN), neuronale Netze
Grundkonzept der Linearen Regression
Bei der linearen Regression geht es darum, eine Linie (oder Hyperplane bei mehreren Prädiktoren) zu finden, die die Beziehung zwischen den Prädiktoren ( X ) und der Zielvariable ( y ) möglichst gut beschreibt.
Die allgemeine Form der Gleichung einer linearen Regression ist:

Anwendung in KI/ML
In KI/ML wird die lineare Regression häufig für folgende Aufgaben verwendet:
1. Vorhersagen (Prediction): Die lineare Regression wird verwendet, um kontinuierliche Werte vorherzusagen. Zum Beispiel kann sie verwendet werden, um die Preise von Häusern basierend auf Merkmalen wie Quadratmeterzahl, Anzahl der Zimmer usw. vorherzusagen.
2. Merkmalsgewichtung (Feature Importance): Die Koeffizienten der linearen Regression können Hinweise darauf geben, welche Merkmale (Features) einen größeren Einfluss auf die Zielvariable haben. Dies ist nützlich, um wichtige Prädiktoren zu identifizieren.
3. Trendanalyse: Lineare Regression kann verwendet werden, um Trends in Daten zu erkennen und zu quantifizieren. Zum Beispiel kann sie verwendet werden, um den Zusammenhang zwischen der Zeit und dem Verkaufsvolumen eines Produkts zu analysieren.
Implementierung einer linearen Regression in Python
Hier ist ein einfaches Beispiel für die Implementierung einer linearen Regression mit der Bibliothek `scikit-learn` in Python:
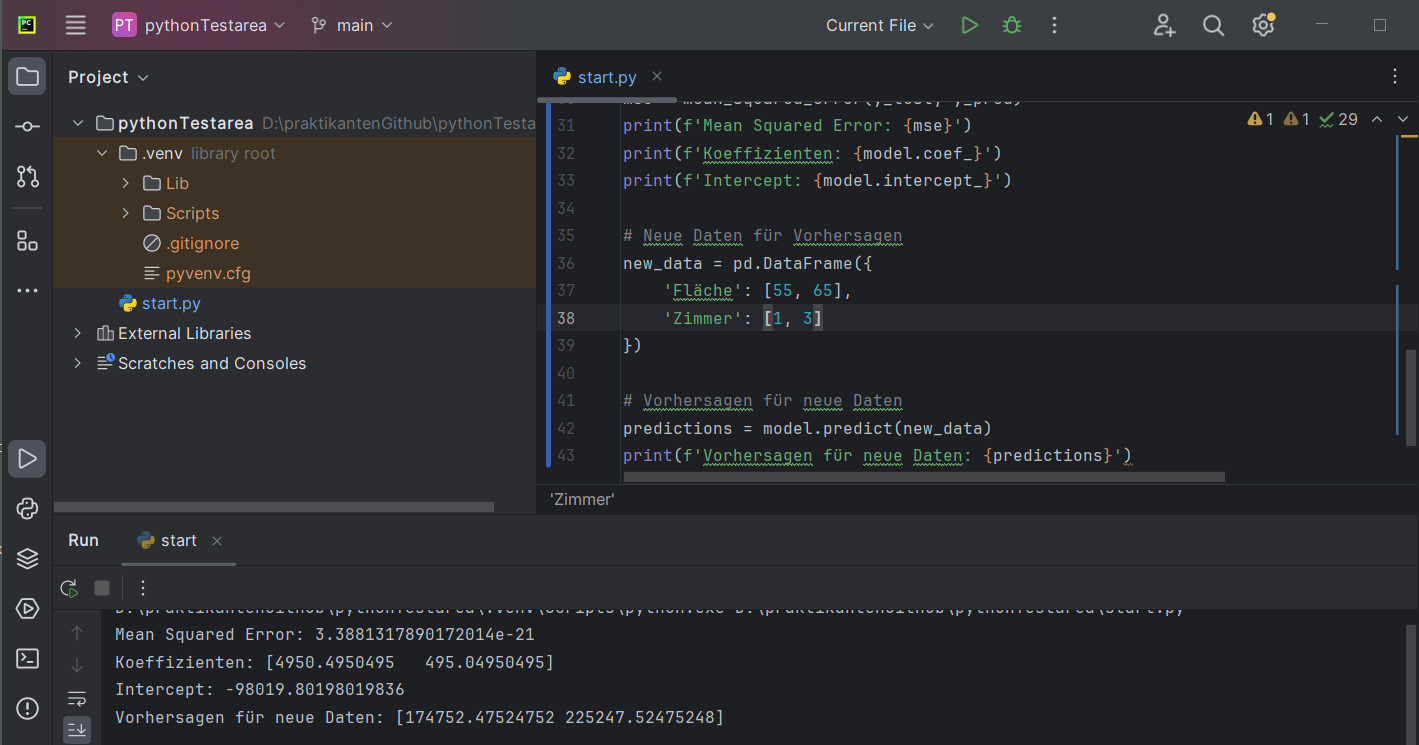
import numpy as npAls Ergebnis der Trainings sind dann Vorhersagen für neue Eingabedaten möglich:
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Beispiel-Daten
data = {
'Fläche': [50, 60, 70, 80, 90],
'Zimmer': [1, 2, 3, 4, 5],
'Preis': [150000, 200000, 250000, 300000, 350000]
}
df = pd.DataFrame(data)
# Merkmale (X) und Zielvariable (y)
X = df[['Fläche', 'Zimmer']]
y = df['Preis']
# Aufteilen der Daten in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Modell erstellen und trainieren
model = LinearRegression()
model.fit(X_train, y_train)
# Vorhersagen treffen
y_pred = model.predict(X_test)
# Modellbewertung
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')
print(f'Koeffizienten: {model.coef_}')
print(f'Intercept: {model.intercept_}')
Wichtige Punkte bei der Linearen Regression in KI/ML
1. Annahmen prüfen: Lineare Regression setzt bestimmte Annahmen voraus, wie Lineare Beziehung, Normalverteilung der Fehler, Homoskedastizität und keine Multikollinearität. Diese sollten überprüft werden, um die Validität des Modells sicherzustellen.
2. Regularisierung: Bei der linearen Regression kann es vorkommen, dass das Modell überangepasst (overfitted) wird, wenn zu viele Merkmale verwendet werden. Techniken wie Ridge- oder Lasso-Regression können zur Regularisierung verwendet werden, um dieses Problem zu mindern.
3. Interpretierbarkeit: Ein Vorteil der linearen Regression ist ihre Interpretierbarkeit. Die Koeffizienten zeigen direkt an, wie stark und in welcher Richtung jedes Merkmal die Zielvariable beeinflusst.
Zuletzt geändert: Montag, 3. Juni 2024, 13:48